概要
2点間の線形補間とは、空間上の2点A,Bを端点とする線分AB上の任意の点の位置を、計算して求めることです。
この考えを用いることによって、直線上に限るがオブジェクトを移動させることが出来ます。
線形補間の応用として、イージングやベジェ曲線の話もしたいと思います。
2点間の線形補間入門
まず内分の公式についておさらいしてみましょう。中学校で習うやつです。
線分$AB$を$m:n$に内分する点$P$とは、線分$AB$上にあって$AP:PB=m:n$となる点のことをいう。
2次元上の点$P$の座標は次の式で求めることができます。
$(Aの座標) = (x_a,y_a), (Bの座標) = (x_b, y_b)$とするとき、
$$
(Pの座標) = \left(\frac{nx_a + mx_b}{m+n}, \frac{ny_a + my_b}{m+n}\right).
$$

[証明]
$x$成分に関して示せば$y$成分に関しても同様である。
点$P$の座標=($x_p$,$y_p$)とおく。線分$AP$の$x$成分の長さは、$|x_p−x_a|$。
また線分$PB$の$x$成分の長さは、$|x_b−x_p|$である。
今,$AP:PB=m:n$なので、
$|x_p−x_a|:|x_b−x_p|=m:n$より比の計算から、$m|x_b−x_p|=n|x_p−x_a|$。
ここで、$x_p$は$x_a$と$x_b$の間にある。つまり$x_a \lt x_b$のときは、$x_a \lt x_p \lt x_b$。
$x_b \lt x_a$のときは、$x_b \lt x_p \lt x_a$となる。
$x_a \lt x_b$のとき、
$$|x_p−x_a|=x_p−x_a, |x_b−x_p|=x_b−x_p.$$
$x_b \lt x_a$のとき、
$$|x_p−x_a|=−(x_p−x_a),|x_b−x_p|=−(x_b−x_p)。$$
$m|x_b−x_p|=n|x_p−x_a|$の絶対値が外せて、$m(x_b−x_p)=n(x_p−x_a)$とできる.
$$mx_p+nx_p=nx_a+mx_b \Rightarrow x_p(m+n)=nx_a+mx_b$$
$$x_p=\frac{nx_a+mx_b}{m+n}$$
を得る.■
この証明により、内分の公式が任意の次元に拡張できることも分かりますね。
さて、上の公式で$m=t$、$n=1-t \quad (0 \leq t \leq 1)$とおいてみます。$m+n=1$より、
$$(点Pの座標)=((1-t)x_a+tx_b,(1-t)y_a+ty_b).$$
となります。
$t=0$のとき、
$$((1-0)x_a + 0x_b, (1-0)y_a+0y_b)=(x_a,y_a)=(点Aの座標).$$
つまり点$A$と点$P$は一致します。
$t=1$のとき、
$$((1-1)x_a + 1x_b, (1-1)y_a+1y_b)=(x_b,y_b)=(点Bの座標).$$
つまり点$B$と点$P$は一致します。
命題
$0 \lt t \lt 1$のとき、$P$は$AB$の内分点になる。
[証明]
任意の内分が$t:1−t$でかけることを示す。
$P$を線分$AB$を$a:b$に内分する点とする。$(\forall a,b \in N)$
比に同じ数をかけても変わらないので、$\frac{1}{a+b}$をかけて、
$a:b=\frac{a}{a+b}:\frac{b}{a+b}$となる.
$t=\frac{a}{a+b}$とおけば、$a \gt 0,b \gt 0$だから、$0 \lt t \lt 1$。
また,$\frac{b}{a+b}=\frac{a+b}{a+b}−\frac{a}{a+b}=1−t$。
よって、$0 \lt t \lt 1$がとれて、$a:b=t:1−t$とかけることが示せた。■
この議論から、$t$を$0$から$1$まで変化させることによって、2点間の線形補間ができることがイメージできます。
実際に補間してみよう
イージングで気持ちいい動きに
イージング関数の明確な定義を見つけることはできませんでしたが、閉区間[0,1]上の数値を良い感じに加工できる関数のことを言います。UIアニメーションなどで視覚効果を得るために使えます。
4で述べるベジェ曲線を用いれば簡単にイージング関数が作れる(かもしれないです)。
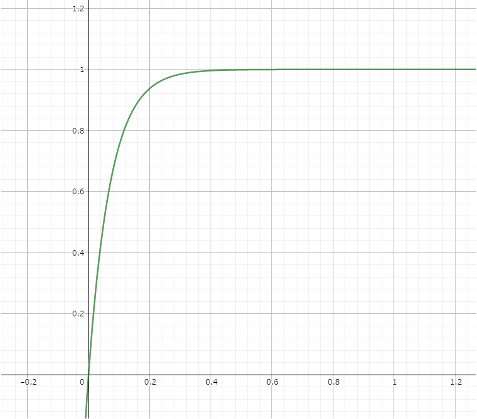
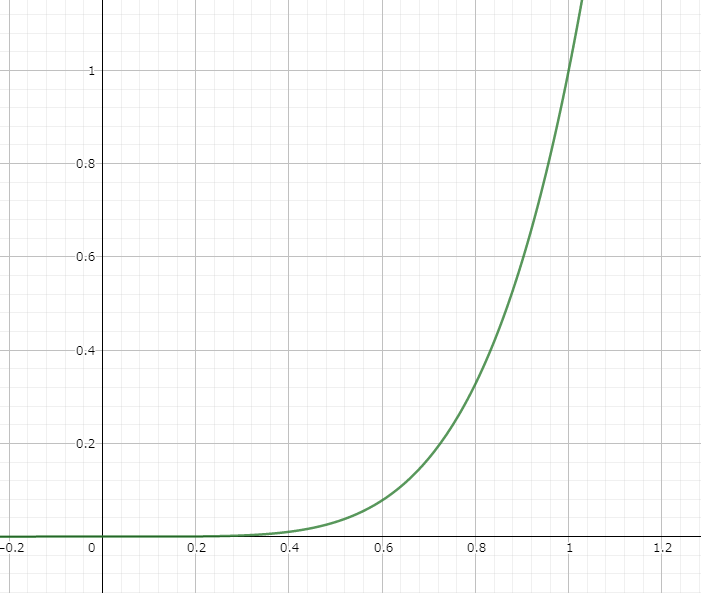
上記2つは以下のようにUIで使用可能です。
ベジェ曲線
内分の応用としてベジェ曲線があげられます。ベジェ曲線はコンピュータで美しく曲線が描けることで知られています。その理論を見ていきましょう。
2次ベジェ曲線
2次ベジェ曲線は$2$点$A,B$と$1$つの制御点$Q$で作ることが出来ます。
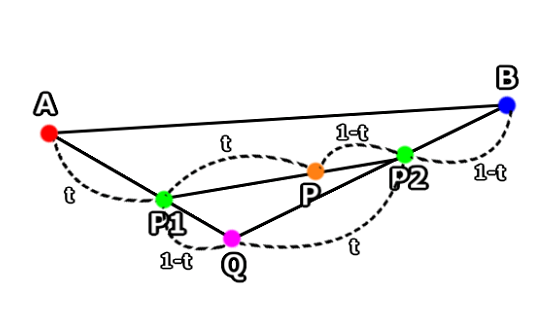
線分$AQ$を$t:1-t$に内分する点を$P_1$、線分$QB$を$t:1-t$に内分する点を$P_2$とします。
線分$P_1P_2$を$t:1-t$に内分する点を$P$として、点$P$の軌跡を2次ベジェ曲線と定義します。
点$A$の座標を$(x_0,y_0)$、点$Q$の座標を$(x_1,y_1)$、点Bの座標を$(x_2,y_2)$とします。
内分の公式から、
$$(点P_1の座標) = ((1-t)x_0 + tx_1, (1-t)y_0 + ty_1), $$
$$(点P_2の座標) = ((1-t)x_1 + tx_2, (1-t)y_1 + ty_2)$$
したがって、$P$の座標も内分の公式から求められて、
$$(t^2(x_2-2x_1+x_0)+2t(x_1-x_0)+x_0,t^2(y_2-2y_1+y_0)+2t(y_1-y_0)+y_0)$$
となります。
3次ベジェ曲線
3次ベジェ曲線は$2$点$A,B$と$2$つの制御点$Q_1,Q_2$で作ることが出来ます。
線分$AQ_1$を$t:1-t$に内分する点を$P_1$、線分$Q_1Q_2$を$t:1-t$に内分する点を$P_2$、
線分$Q_2B$を$t:1-t$に内分する点を$P_3$とします。
さらに、線分$P_1P_2$を$t:1-t$に内分する点を$P_4$、線分$P_2P_3$を$t:1-t$に内分する点を$P_5$とします。
最後に、線分$P_4P_5$を$t:1-t$に内分する点を$P$として、点$P$の軌跡を3次のベジェ曲線と定義します。
$A$の座標を$(x_0, y_0)$、$Q_1$の座標を$(x_1,y_1)$、$Q_2$の座標を$(x_2,y_2)$、$B$の座標を$(x_3,y_3)$とすると、
内分の公式を用いて順番に点の座標を計算していけば、最終的に点$P$の座標、
$(t^3(x_3-3x_2+3x_1-x_0)+t^2(3x_2-6x_1+3x_0)+t(3x_1-3x_0)+x_0,$
$t^3(y_3-3y_2+3y_1-y_0)+t^2(3y_2-6y_1+3y_0)+t(3y_1-3y_0)+y_0)$
を得ることが出来ました。
n次のベジェ曲線
$n$次のベジェ曲線は次のように与えられます。
$A(x_0,y_0),B(x_n,y_n),Q_k(x_k,y_k)(k=1,2,\cdots ,n-1)$と各々座標をおくと、$n$次ベジェ曲線は
$$(\sum_{l=0}^n(nC_lt^l(\sum{k=0}^l(-1)^k\,lC_kx{l-k})), $$
$$\sum_{l=0}^n(nC_lt^l(\sum{k=0}^l(-1)^k\,lC_ky{l-k})))$$
の軌跡で与えられます。(と思っている)
実際には3次のベジェ曲線をいくつも組み合わせて使う場合が一般的なようです。
コメント