概要
暗号とは、当事者間にだけ分かる記号のことで、秘密を守ることが主な使用目的です。今回は特にRSA暗号方式に関して書いていきます。
RSA暗号方式とは
RSA暗号は、ロナルド・リベスト(R)、アディ・シャミア(S)、レオナルド・エーデルマン(A)の3人によって1977年に発明されました。素因数分解は難解であるが、2つの素数の積を求めることは簡単であるということを利用した暗号方式です。
例えば、$8635844967113809$の素因数分解は困難ですが、$89652331×96325939$を計算するのは人の手でやってもすぐに求まりますね。
公開鍵暗号
RSA暗号は公開鍵暗号方式です。公開鍵と並立して共通鍵方式というものもあります。
まず共通鍵方式について。共通鍵方式とは、暗号化と複合化を同じ鍵で行う暗号方式のことです。
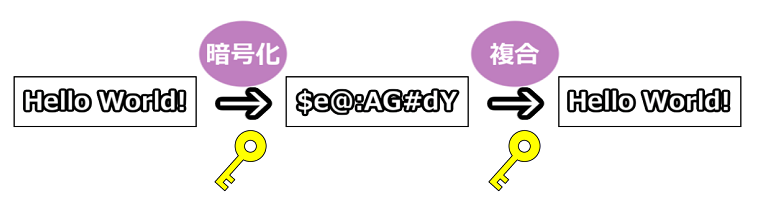
当然、鍵は双方が知っている必要があるので交換が必須です。その際、第三者にカギを複製されたら簡単に暗号を複合出来てしまうことになるので注意が必要です。
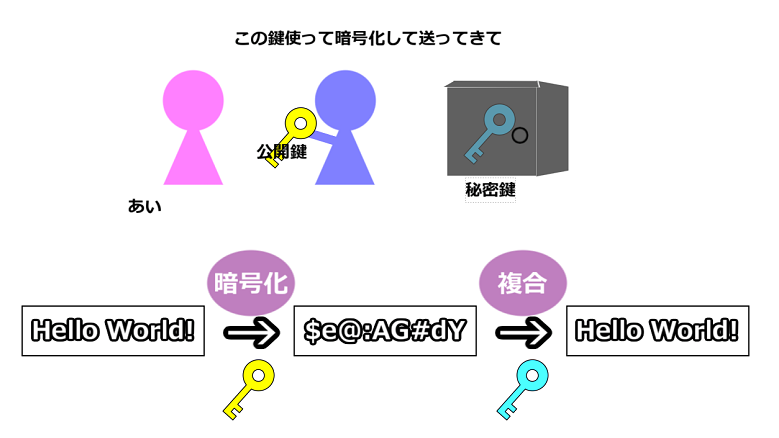
鍵の交換のリスクを限りなくなくしたのが公開鍵方式です。公開鍵暗号方式では受信側が公開鍵と秘密鍵の2種類の鍵を発行します。公開鍵を用いて通信相手に暗号化してもらい、自分の元に届いた暗号文を、自分だけが知る秘密鍵で複合します。
RSAの理論
RSAの理論の根底はフェルマーの小定理です。(“小定理”と銘打っているが非常に重要な定理ですよ!)
定理(フェルマーの小定理)
$p$を素数とする。このとき、$p$の倍数でない任意の整数$a$に対して、
$$a^{p-1} \equiv 1 \pmod p$$
が成り立つ。
簡単に言えば、$p$の倍数でない整数を$p-1$乗すると、$p$で割って$1$余る数になるということです。この定理から1つの正しい命題が得られます。
命題
$p,q$を互いに異なる素数とする。$f$は$f \equiv 1 \pmod{(p-1)(q-1)}$を満たす整数とする。このとき任意の整数$m$に対して、
$$m^f \equiv m \pmod{pq}$$
が成り立つ。
[証明]
$p$と$q$は互いに素だから$m^f \equiv m \pmod p$かつ$m^f \equiv m \pmod q$を示せればよい。
$f \equiv 1 \pmod{(p-1)(q-1)}$より、整数$k$が存在して$f = (p-1)(q-1)k + 1$とかける。
フェルマーの小定理より、$m^f = m^{(p-1)(q-1)k + 1} \equiv 1^{(q-1)k} \cdot m \equiv m \pmod p$
$q$についても同じ。■
RSA暗号はこの命題を用います。手順は以下の通りです。
- 文字列を数値に変換する方法を考える。(例:A~Zに0~25の番号を対応させる方法。
「ABCD」→「$0^1 + 1^2 + 2^3 + 3^4 = 90$」) - メッセージの数値の最大を決める。(上の例で$k$文字だとすると、最大値は$26^k$である。)
- 素数$p,q$を決める。このとき、積$n = pq$は2で決めた最大値よりも大きく取らなければならない。(複合出来なくなるため)
$p$と$q$は公開せず、積$n$だけを公開するようにする。 - 整数$e$を$gcd(e,(p-1)(q-1))=1$
($e$と$(p-1)(q-1)$の最大公約数が1ということ)となるようにランダムにとる。 - 整数$d$を$de \equiv 1 \pmod{(p-1)(q-1)}$となるようにとる。
(ユークリッドの互除法を使えばすぐ求まる)
ここまでを行った後、公開鍵として$n$と$e$の数値の組を、秘密鍵として$n$と$d$の数値の組とそれぞれ定めます。
メッセージの数値が$m$であるものを送ったとしましょう。まず送信側は公開鍵で暗号化します。
$m^e$を$n$で割った余りを$c$とし、この$c$を受信側に送り付けます。受信側は$c$を秘密鍵で複合します。$c^d$を$n$で割った余りがまさに$m$となります。
$$m^e \equiv c \pmod{pq} \rightarrow c^d \equiv m^{de} \equiv m \pmod{pq}$$
最後の合同式は命題からすぐ分かりますね。
簡略化したRSAで実際に見てみる
“RSA”を暗号化、複合してみよう。$p=757, q=951, n=757 \cdot 951=719907, e=431, d=694871$
“RSA” $= 17^1 + 18^2 + 0^3 = 341$
暗号化:$341^{431} \equiv 220 \pmod n$
複合 :$220^{694871} \equiv 341 \pmod n$
確かに複合出来た。(満身創痍)

コメント